Question

A drugstore sells the same brand of talcum powder in two types of cylindrical cans: Can A has a diameter of 5.4 centimeters and a height of 9 centimeters and sells for $3.18. Can B has a diameter of 6.2 centimeters and a height of 12.4 centimeters and sells for $5.98. Which can is the better buy?

Answer 1

We have to find which is the better buy.

This will be the can with the higher amount per volume per dollar.

Then, we have to calculate the volume for each can.

Can A has a diameter of 5.4 cm and a height of 9 cm.

The volume will be the area of the base times the height, so we can calculate it as:

`\begin{gathered} V_a=A_bh \\ V_a=((\pi D^2)/(4))h \\ V_a=(\pi\cdot(5.4)^2)/(4)\cdot9 \\ V_a=(\pi\cdot29.16\cdot9)/(4) \\ V_a=65.61\pi \\ V_a\approx206 \end{gathered}`

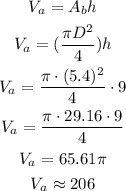
Then, as the price is $3.18, the volume per dollar for can A is:

`v_a=(V_a)/(p_a)=\frac{206\text{ cm}^3}{3.18\text{ usd}}\approx64.78(cm^3)/(usd)`

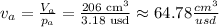
We can do the same for can B.

It has a diameter of 6.2 cm and a height of 12.4 cm, so its volume is:

`\begin{gathered} V_b=(\pi D^2)/(4)h \\ V_b=(\pi\cdot6.2^2)/(4)\cdot12.4 \\ V_b=(\pi\cdot38.44\cdot12.4)/(4) \\ V_b=119.164\pi \\ V_b\approx374 \end{gathered}`

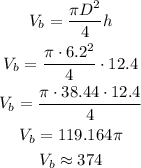
As the price is $5.98, we can calculate the volume per can for B as:

`v_b=(V_b)/(p_b)=\frac{374\text{ cm}^3}{5.98\text{ usd}}\approx62.54(cm^3)/(usd)`

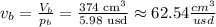
As can A has more volume per dollar than B, it is a better buy.

Answer: Can A is a better buy than can B.