Question

A rectangular piece of metal is 5 in longer than it is wide. Squares with sides 1 in long are cut from the four corners and the flaps are folded upward to form an openbox. If the volume of the box is 300 in, what were the original dimensions of the piece of metal?What is the original width in inches?

Answer 1

Given

The length (l) is 5in longer than it's width

Volume of the box = 300 in

The diagram below illustrates the problem:

The volume (V) of a cuboid which is the volume of the box can be found using the formula:

`V=\text{ l}*\text{ b }*\text{ h}`

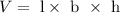
Substituting the given sides and volume:

`\begin{gathered} 300\text{ = \lparen3 + w\rparen }*\text{ \lparen w -2\rparen }*\text{ 1} \\ 3w\text{ -6 + w}^2\text{ -2w = 300} \\ w^2\text{ -w -6 = 300} \\ w^2\text{ - w -306 = 0} \\ (w\text{ + 17\rparen\lparen w - 18\rparen = 0} \\ \\ w\text{ - 18 = 0} \\ w\text{ = 18} \end{gathered}`

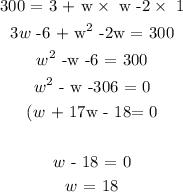
Hence, the width of the rectangular piece is 18 in

The length(l) of the rectangular piece:

`\begin{gathered} l=\text{ 5 + w} \\ =\text{ 5 + 18} \\ =\text{ 23} \end{gathered}`

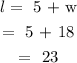
Hence, the dimensions of the piece of metal is 23 in by 18 in

Answer Summary

The original width is 18 in