Since your question doesn't specify which angle is 40 degrees, we will take two cases:
i) When ∠B = 40°
ii) When ∠A = 40°
Solving part (i):
If ∠B = 40°, we can draw a diagram,
Using sine, we can find AB and using tangent, we can find BC.
The ratio and steps to solve are shown below:
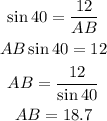
and,
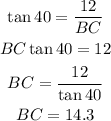
Answer
When ∠B = 40°,AB = 18.7BC = 14.3----------------------------------------------------------------------------------Solving part (ii):
If ∠A = 40°, we can draw a diagram,
Using cosine, we can find AB and using tangent, we can find BC.
The ratio and steps to solve are shown below:
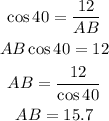
and,
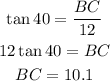
Answer
When ∠A = 40°,AB = 15.7BC = 10.1