Since ABCD is a rectangle, the sides AB and AD are perpendicular.
The slopes of perpendicular segments or lines have the following relation:
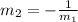
The equation for the line AB is in the slope-intercept form: y = mx + b.
Therefore we can identify its slope: m1 = 2/3.
Now, calculating the slope m2 of line AD, we have:
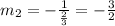
Therefore the slope of line AD is equal to -3/2.