ANSWER
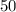
Step-by-step explanation
A coterminal angle to an angle is one that terminates in the same position or on the same side as the angle considered.
Since we are looking for a coterminal angle between 0 and 360, we have to keep subtracting a full revolution (360 degrees) from the given angle until we get an angle that satisfies the condition.
Therefore, we have:

Since 410 is not less than 360, subtract 360 degrees again:

That is the measure of the angle, a, that is coterminal with the given angle.