Question

Determine if the pair of solids is similar. If yes give the scale factor

Answer 1

This solids are similars if the quotients between their correspondent sides are all the same. In this cases the quotients would be:

`(39)/(26),\text{ }(15)/(10)\text{ and }(42)/(28)`

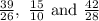
If you calculate those quotients you'll see that they all give 1.5 so the first question is answered, the solids are similar.

The scale factor determinates the relationship between two similar solids or geometric figures. It's usually used while constructing scale models of bigger things like building. To calculate we are going to use the rule of three since the factor tells how many inches in one solid represents an inch in the other one.

We know that 28 inches in the smaller one represent 42 in the bigger one so:

28 in --------- 42 in

1 in ------------ x

Where:

`x=(1\cdot42)/(28)=1.5`

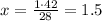
So the value of the quotients I mentioned before is the scale factor of this pair of solids and it's 1.5