Question

This is a 2 part 1 question each part on how to stop a zombie apocalypse by coming up with functions that model the spread of zombies and finding key points in time using your function. (If we get through this entire section: I will write a very long letter of gratitude and give you the highest rating for helping me understand. I truly just want to finish) There are only 2 steps, so this should be easy, but I need help! (Total of questions: 2) Please include some work and a bit of an explanation, so I know how to approach more problems like this. ( Some of these numbers are rather large, so I’ve been using the web2.0 calculator to hold the numbers- making it easy on myself ) In order to get a continue the study of the spread of zombies, you obtain this information: -locals inform you that they seen them stumbling in tattered clothes and causing a disturbance at a local cemetery , where the zombies were found has 100 plots, which are all filled. -Doctor states that his studies indicate that these zombies can spread at a rate of 20% -We know that the population of the U.S is 325,000,000. Therefore, the population of zombies in the country CANNOT exceed that number. (There is a limit to the population that the zombies can reach, so the growth much be modeled by logistic growth. ) •L (x) = a/1+ be^-rx•Let a represent the capacity of the population, must be positive •Let r represent a positive real number for the growth rate •Let x be the independent variable representing the elapsed time •B is a real number constantIN your function the independent variable •x, will be in the number of daysHERE IS WHAT I HAVE SO FAR : * A=350,000,000* R in decimal form = 0.2* L(0)= 100 - assuming that all of the people buried in the cemetery were re animated, the L(x) is equal to 100, as x=0, being the time in days , when everything started. * L(x) =325,000,000/1+3,249,999e^-0.2x (This is the logistic growth function for the growth of the zombie population) I will send you a picture of itNOW that that’s out of the way, HERE IS WHAT I NEED MOVING FORWARD: (Please include a small explanation, so I can read it and understand what is going on.) Step 2: population reaches 50% using the function to find how many days it will take the zombies to infect half of the population. (Use the function you created to find how long it will take) 1. How long will it take for the zombie population to equal half of the total population? How did you get that answer ? Step 3 : Critical Threshold using the function to find how many days it will take for the human population to drop below the point of no return(In order to come up with a plan to stop the zombie apocalypse, the task force needs you to know how long they have before the zombie population reaches critical point of 80% of the total population. Use the function you created to find how long this will take. ) 1. How long will it take for the zombie population to equal 80% of the total population? What did you do to get this?

Answer 1

`L(x)=(325000000)/(1+3249999e^(-0.2x))=(3.25\cdot10^8)/(1+3.249999\cdot10^6e^(-0.2x))`

Where x is the time, as you know

As for step 2:

First, we determine half of the total population that can get infected, this is simply:

`(325000000)/(2)=1.625*10^8`

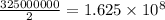
I'll use scientific notation since it is much easier to work in this way

`\Rightarrow L(half_(population))=1.625\cdot10^8=(3.25\cdot10^8)/(1+3.249999\cdot10^6e^(-0.2x))`
`\begin{gathered} \Rightarrow1+3.249999\cdot10^6e^(-0.2x)=(3.25\cdot10^8)/(1.625\cdot10^8)=2 \\ \Rightarrow3.249999\cdot10^6e^(-0.2x)=1 \\ \Rightarrow e^(-0.2x)=3.249999\cdot10^(-6) \end{gathered}`

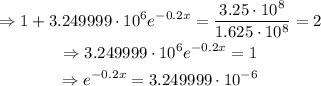
Remember the next property of the exponential function:

`\ln (e^x)=x;x\in\mathfrak{\Re }`
`\begin{gathered} \Rightarrow-0.2x=\ln (3.249999\cdot10^(-6)) \\ \Rightarrow x=-\ln (3.249999\cdot10^(-6))(1)/(0.2)\approx6.32 \end{gathered}`

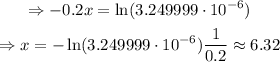
So, in 6.32 days it is expected that half the population will be infected.

Regarding Part C, which is quite similar to Part B, we only need to exchange 50% by 80%

80% of the population corresponds to:

`\text{Total}_{\text{population}}\cdot0.8=2.6\cdot10^8`
`\Rightarrow L(80percent)=2.6\cdot10^8=(3.25\cdot10^8)/(1+3.249999\cdot10^6e^(-0.2x))`
`\begin{gathered} \Rightarrow1+3.249999\cdot10^6e^(-0.2x)=(3.25\cdot10^8)/(2.6\cdot10^8)=1.25 \\ \Rightarrow e^(-0.2x)=1.25\cdot3.249999\cdot10^(-6) \\ \Rightarrow x=-(1)/(0.2)\ln (1.25\cdot3.249999\cdot10^(-6)) \end{gathered}`

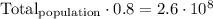
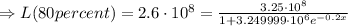
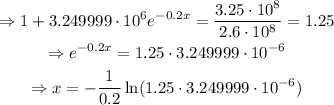
Finally,

`x\approx62.07`

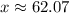
The point of no return will be reached in 62 days, approximately

Now, regarding part 4

So, 100 people left

If there are only 100 people, then there are 3.25x10^8-100 zombies.

`\Rightarrow L(100people)=3.25\cdot10^8-100=(3.25\cdot10^8)/(1+3.249999\cdot10^6e^(-0.2x))`
`\begin{gathered} \Rightarrow3.25\cdot10^8-100=(3.25\cdot10^8)/(1+3.249999\cdot10^6e^(-0.2x)) \\ \Rightarrow1+3.249999\cdot10^6e^(-0.2x)=(3.25\cdot10^8)/(3.25\cdot10^8-100)\approx1.00000031 \end{gathered}`
`\begin{gathered} \Rightarrow3.249999\cdot10^6e^(-0.2x)=0.00000031=3.1\cdot10^(-7) \\ \Rightarrow e^(-0.2x)\approx9.54\cdot10^(-14) \end{gathered}`
`\Rightarrow x=-(1)/(0.2)\cdot\ln (9.54\cdot10^(-14))\approx149.904`

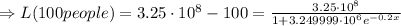
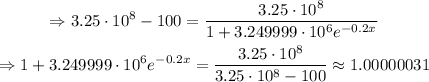
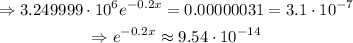
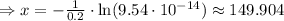
Therefore, 100 humans will be left after approximately 150 days

About the process, the only thing we did was to substitute the value of L(x) for the corresponding percentage (50%,80%,100 humans left) and solve for x.

You can interpret the function in this way:

`L(x)=(3.25\cdot10^8)/(1+3.249999\cdot10^6e^(-0.2x))=\frac{a}{1+be^(-0.2x)^{}}=a(1+be^(-0.2x))^(-1)`

The only notable factor is the exponential function, as x increases, we obtain:

`\begin{gathered} x\rightarrow\infty \\ \Rightarrow-0.2x\rightarrow-\infty \\ \Rightarrow e^(-0.2x)\rightarrow e^(-\infty)\rightarrow0 \end{gathered}`

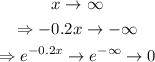
However, that function is never zero. It's only a limit

So, there will always remain at least a fraction of a human left.

That from a mathematical point of view, the physical reality would be different.