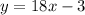Question

Solve for y in terms of xSolve for y:1/3y=6 (x- 1/6)

Answer 1

You have the following equation given in the exercise:

`(1)/(3)y=6(x-(1)/(6))`

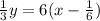
In order to solve for "y" in terms of "x", you can follow the steps shown below:

1. Apply the Distributive property, which states:

`\begin{gathered} a(b+c)=ab+ac \\ a(b-c)=ab-ac \end{gathered}`

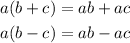
Then:

`\begin{gathered} (1)/(3)y=(6)(x)-(6)((1)/(6)) \\ \\ (1)/(3)y=6x-1 \end{gathered}`

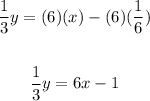
2. Now you must apply the Multiplication property of equality by multiplying both sides of the equation by 3:

`\begin{gathered} ((1)/(3)y)(3)=(6x-1)(3) \\ \\ y=18x-3 \end{gathered}`

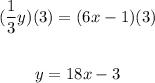
Therefore, the equation solved for "y" in terms of "x", is:

`y=18x-3`