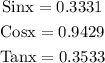Question

Using the triangle below. Answer the following questions. 3. What is the sine of x?4. What is the cosine of x?5. What is the tangent of x?

Answer 1

Step-by-step explanation

The triangle below is a right-angle triangle, where the adjacent side is 150ft and the opposite side is 53ft.

We can get the opposite side using the formula below;

`(\text{Hypotenuse)}^2=(Opposite\text{)}^2+(\text{Adjacent)}^2`

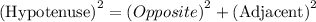
We will then have;

`\begin{gathered} (\text{Hypotenuse)}^2=150^2+53^2 \\ \text{Hypotenuse}=\sqrt[]{25309} \\ \text{Hypotenuse}=159.088 \end{gathered}`

Using the trigonometric functions we will have the following;

`\begin{gathered} \text{Sinx}=\frac{\text{opp}}{Hyp}=(53)/(159.088)=0.3331 \\ \text{Cosx}=\frac{\text{Adj}}{Hyp}=(150)/(159.088)=0.9429 \\ \text{Tanx}=\frac{\text{opp}}{Adj}=(53)/(150)=0.3533 \end{gathered}`

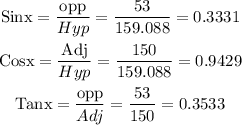
Answer:

`\begin{gathered} \text{Sinx}=0.3331 \\ \text{Cosx}=0.9429 \\ \text{Tanx}=0.3533 \end{gathered}`