Question

A quadratic function f(x)f(x) is hidden from view. You must find the xx-intercept(s) of f(x)f(x) and write the answer(s) in the form (x,y)(x,y). Choose the form of the quadratic function f(x)f(x) that you would like to see in order to answer the question most efficiently.

Answer 1

f(x) should be in canonical form. So it must have the form

`f(x)=a(x-x_v)^2+y_v`

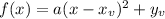
Where a is the main coefficient and is the vertex

Explanation:

A quadratic function has a unique extreme value in its vertex. That value might be a maximum or a minimum depending on the sign of the main coefficient of the quadratic function. In order to quickly obtain the vertex, the quadratic must be written in canonical form. That means that f(x) must have the form

`f(x)=a(x-x_v)^2+y_v`

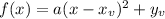
Where a is the main coefficient (which should be negative so that a minimum exists in the first place) and is the vertex. If f(x) is written in that form, then it will be easier to find the minimum of f(x), which is the vertex

Hence for the quadratic function below

`\begin{gathered} f(x)=(x-2)^2-9 \\ f(x)=x^2-4x-5 \\ ax^2+bx+c \\ a=1,\text{ b=-4, c=-5} \\ x_v=-(b)/(2a) \\ x_v=(-(-4))/(2(1)) \\ x_v=(4)/(2) \\ x_v=2 \\ y_v=2^2-4(2)-5 \\ y_v=-9 \\ (x,y)\longrightarrow(2,-9) \end{gathered}`

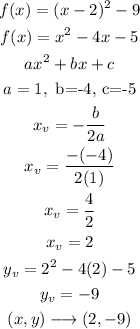
Hence there is only one x- intercept and answer is (2, -9)