Question

Find the measure of an interior angle of a polygon with 20 diagonals

Answer 1

The number of diagonals and number of sides of a polygon are related with the formula

`\begin{gathered} no\text{. of diagonals = }(n(n-3))/(2) \\ \text{Where n = number of sides of the polygon } \end{gathered}`

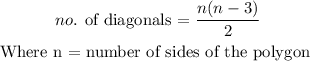
Substituting we have

`\begin{gathered} no\text{. of diagonals = }(n(n-3))/(2) \\ 20\text{ = }(n(n-3))/(2) \\ 20=(n^2-3n)/(2) \\ \text{cross multiplying we have } \\ n^2-3n=20*2 \\ n^2-3n=40 \\ n^2-3n-40=0 \end{gathered}`

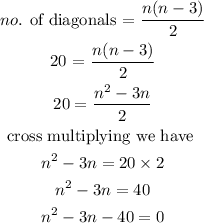
Solving the quadratic equation for n, we have

`\begin{gathered} n^2-3n-40=0 \\ n^2-8n+5n-40=0 \\ n(n-8)+5(n-8)=0 \\ (n+5)(n-8)=0 \\ \text{Either } \\ n+5=0 \\ n=-5\text{ } \\ Or \\ n-8=0 \\ n=8 \end{gathered}`

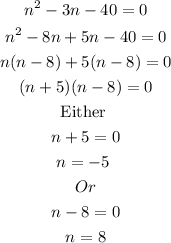
So, we will go with n = 8, since the number of sides cannot be a negative number.

Now, sum of interior angles in a regular polygon is given by

`\begin{gathered} S=180(n-2) \\ \text{Where S = sum and n = numbers } \end{gathered}`

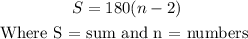
So we have

`\begin{gathered} S=180(n-2) \\ S=180(8-2) \\ S=180*6 \\ S=1080\text{ } \end{gathered}`

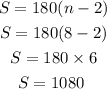
So, the measure of an interior angle becomes

`\begin{gathered} (S)/(n) \\ =(1080)/(8) \\ =135\degree \end{gathered}`

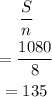
Hence the answer is 135 degrees