Question

Malachi is practicing math fluency. He has 100 math operations flashcards with 42 addition problem cards, 56 subtraction cards, and 2 multiplication cards. He will time himself to see how fast he can solve the problems on two cards. He chooses his two cards and they are both multiplication cards. Is choosing two multiplication cards likely? Explain by running a simulation. Part A: Describe the process for one repitition, including possible outcomes, assigned repititions, and measured variables.Part B: use digits from a table of random digits or use your calculator to perform one repitition. Submit the list of random digits and indicate those that represent multiplication cards.Part C: Suppose there were 5 times when both cards selected were multiplication cards after 1,500 repititions of the simulation. state your conclusions from these results.

Answer 1

He chooses his two cards and they are both multiplication cards. Is choosing two multiplication cards likely?

Let:

A = Draw an addition card

B = Draw a subtraction card

C = Draw a multiplication card

N = Total number of cards

`\begin{gathered} P(A)=(42)/(100)=4.2 \\ P(B)=(56)/(100)=5.6 \\ P(C)=(2)/(100)=0.02 \\ P(C|C)=(P(C\cap C))/(P(C))=0.02 \end{gathered}`

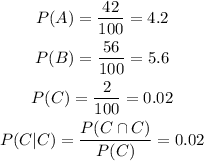
Choosing two multiplication cards is very unlikely, the probability of that is only 2%.

Part A:

There are many possibilities, for example:

Draw an addition card and draw a subtraction card:

`P(B|A)=(P(A\cap B))/(P(B))`

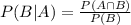
The possibles outcomes can be found using a permutation:

`\begin{gathered} P(n,r)=nPr=(n!)/((n-r)!) \\ P(3,2)=3P2=(3!)/((3-2)!) \\ P(3,2)=6 \end{gathered}`

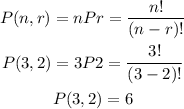
The measured variables are:

P(A) = Probability of draw an addition card

P(B) = Probability of draw a subtraction card

P(C) = Probability of draw a multiplication card

P(A ∩ B) = Probability of draw an addition card and a subtraction card

P(B ∩ C) = Probability of draw a subtraction card and a multiplication card

P(A ∩ C) = Probability of draw an addition card and a multiplication card