The sequence given is a geometric sequence.
A geometric sequence has the explicit formula in the form:
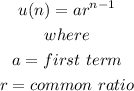
and the recursive formula in the form:
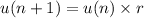
The question provides the following parameters:
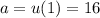
The recursive formula is given to be:
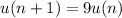
Therefore, the common ratio is:
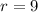
Hence, the explicit formula is given to be:
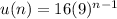
OPTION B is correct.