1 Answer

Binita Lama · Answer 1 · 2023-12-16T02:15:53+0000

a. We are told that 3/5 of the devotional books are bible storybooks.

Also, he will move to the display table 1/2 of that fraction.

So, to find the final fraction part of the children's devotional books he moves, we need to find 1/2 of 3/5.

So, we need to multiply the fraction 1/2 by the fraction 3/5:

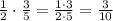
$(1)/(2)\cdot(3)/(5)=(1\cdot3)/(2\cdot5)=(3)/(10)$

Thus, the fraction part is

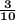
$\mathbf{(3)/(10)}$

b. Now, notice that the total of devotional books is 100. So, we need to find 3/10 of 100. We do so by multiplying that fraction by 100:

$(3)/(10)\cdot100=3\cdot(100)/(10)=3\cdot10=30$

Therefore, the number of bible storybooks he moved to the display table is 30.

Please log in or register to add a comment.