we must find the for each fuction and we can say from it if they are parellel or perpendicular
F(x)
slope

(x2,y2)=(3,-1) and (x1,y1)=(2,4)
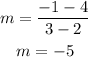
G(x)
(x2,y2)=(2,6) and (x1,y1)=(-3,7)
slope
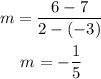
when the slopes are equals the lines are parellel so This is not the case
when the slopes one is the other inverted and with a different sign they are parellel so this is not the case
So, the solution is neither