Given,
The mass of the satellite, m=100 kg
The radius of the initial orbit, r=7.5×10⁶ m
The radius of the final orbit of the satellite, R=7.7×10⁶ m
The mass of the earth, M=5.97 x 10²⁴ kg
The gravitational constant, G= 6.67 x 10⁻¹¹ Nm²/kg²
From Newton's universal law of gravitation, the gravitational force on the satellite when it is in the initial orbit is given as
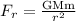
On substituting the known values in the above equation,
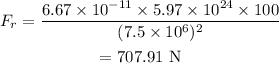
The gravitational force on the satellite, when it is on its final orbit is given by,
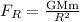
On substituting the known values in the above equation,
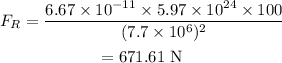
The change in the force is given by,
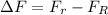
On substituting the known values,
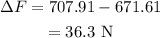
Thus the gravitational force from the Earth decreases by 36.3 N after the satellite changes its orbit.