Question

11) Using the law of sines, determine whether the given information results in one triangle, two triangle or no triangle at all. Solve any triangle that results. a=26b = 29Angle A =58 degree

Answer 1

To determine the number of solutions, let us first solve for h.

`\begin{gathered} h=a\sin B \\ h=26(\sin29) \\ h=12.6 \end{gathered}`

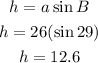
We will also need to find b using the sine law.

`\begin{gathered} (a)/(sinA)=(29)/(sinB) \\ \\ (26)/(sin58)=(29)/(sinB) \\ \\ \sin B=(29(\sin58))/(26) \\ \sin B=0.946 \\ \sin^(-1)(\sin B)=\sin^(-1)0.946 \\ B=71.07 \end{gathered}`

Here we see that a = 26, b = 29, and h = 12.6.

When h < a < b, then are 2 solutions or 2 triangles.

Next, we solve for the 2 solutions.

For the first solution, we already calculated B to be 71.07 degrees. We know that A = 58 degrees. So to find C, we simply subtract their sum from 180.

`180-(58+71.07)=50.93`

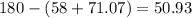
Again, using the sine law, we can solve for c.

`\begin{gathered} (a)/(sinA)=(c)/(sinC) \\ \\ (26)/(sin58)=(c)/(sin50.93) \\ \\ c=(26(sin50.93))/(sin58) \\ \\ c=23.80 \end{gathered}`

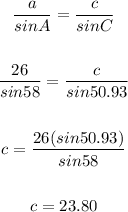
The other solution is when B = 180 - 71.07 = 108.93. We do this because there are 2 angle measurements that have the same sine (in this case, it's 0.946).

Again, the other possible value of B is 180 - 71.07 or 108.93. That will give us C = 180 - (53 + 108.93) = 18.07 degrees.

Again, we use the sine law to solve for the corresponding c.

`\begin{gathered} (26)/(\sin58)=(c)/(\sin18.07) \\ \\ c=(26(\sin18.07))/(\sin58) \\ \\ c=9.51 \end{gathered}`

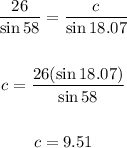
So the answers are:

1. There are 2 possible triangles.

2. Triangle 1: B = 71.07 degrees, C = 50.93 degrees, and c = 23.80.

3. Triangle 2: B = 108.93 degrees, C = 18.07 degrees, and c = 9.51