SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the given set of values
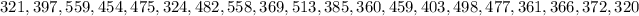
STEP 2: Write the formula for calculating the Standard deviation of a set of numbers
![\begin{gathered} S\tan dard\text{ deviation=}\sqrt[]{\frac{\sum^{}_{}(x_i-\bar{x})^2}{n-1}} \\ where\text{ }x_i\text{ are data points,} \\ \bar{x}\text{ is the mean} \\ \text{n is the number of values in the data set} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/t60dheil1h44m4mjqixrvy2udihnj76es7.png)
STEP 3: Calculate the mean
![\begin{gathered} \bar{x}=\frac{\sum ^{}_{}x_i}{n} \\ \bar{x}=\frac{\sum ^{}_{}(321,397,559,454,475,324,482,558,369,513,385,360,459,403,498,477,361,366,372,320)}{20} \\ \bar{x}=(8453)/(20)=422.65 \end{gathered}]()
STEP 4: Calculate the Standard deviation
![\begin{gathered} S\tan dard\text{ deviation=}\sqrt[]{\frac{\sum^{}_{}(x_i-\bar{x})^2}{n-1}} \\ \sum ^{}_{}(x_i-\bar{x})^2\Rightarrow\text{Sum of squares of differences} \\ \Rightarrow10332.7225+657.9225+18591.3225+982.8225+2740.52251+9731.8225+3522.4225+18319.6225+2878.3225 \\ +8163.1225+1417.5225+3925.0225+1321.3225+386.1225+5677.6225+2953.9225+3800.7225 \\ +3209.2225+2565.4225+10537.0225 \\ \text{Sum}\Rightarrow108974.0275 \\ \\ S\tan dard\text{ deviation}=\sqrt[]{(111714.55)/(20-1)}=\sqrt[]{(111714.55)/(19)} \\ \Rightarrow\sqrt[]{5879.713158}=76.67928767 \\ \\ S\tan dard\text{ deviation}\approx76.68 \end{gathered}]()
Hence, the standard deviation of the given set of numbers is approximately 76.68 to 2 decimal places.
STEP 5: Calculate the First and third quartile
![\begin{gathered} \text{IQR}=Q_3-Q_1 \\ \\ To\text{ get }Q_1 \\ We\text{ first arrange the data in ascending order} \\ \mathrm{Arrange\: the\: terms\: in\: ascending\: order} \\ 320,\: 321,\: 324,\: 360,\: 361,\: 366,\: 369,\: 372,\: 385,\: 397,\: 403,\: 454,\: 459,\: 475,\: 477,\: 482,\: 498,\: 513,\: 558,\: 559 \\ Q_1=((n+1)/(4))th \\ Q_1=((20+1)/(4))th=(21)/(4)th=5.25th\Rightarrow(361+366)/(2)=(727)/(2)=363.5 \\ \\ To\text{ get }Q_3 \\ Q_3=((3(n+1))/(4))th=(3*21)/(4)=(63)/(4)=15.75th\Rightarrow(477+482)/(2)=(959)/(2)=479.5 \end{gathered}]()
STEP 6: Find the Interquartile Range
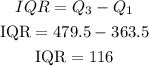
Hence, the interquartile range of the data is 116