Question

practice help!What is the equation of g in terms of f?A. g(x) = f(x)B. g(x) = -f(x)C. g(x) = f(-x)D. g(x) = -f(-x)

Answer 1

To answer this question, we can proceed as follows:

1. We can find the equation for the quadratic function, f(x) (solid line). To do this, we can use the vertex form of quadratic functions as follows:

`f(x)=a(x-h)^2+k`

Where (h, k) is the vertex of the parabola. From the graph, we have that the vertex is (1, -4). We can also see that the y-intercept of this quadratic function is (0, -3). Then with this information, we can find the equation of the function as follows:

`f(x)=a(x-1)^2+(-4)\Rightarrow f(x)=a(x-1)^2-4`

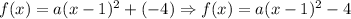
Now, to find the value of as follows:

1. f(0) = -3

`-3=a(0-1)^2-4\Rightarrow-3=a(-1)^2-4\Rightarrow-3=a(1)-4`

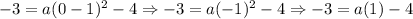
Then, we have:

`-3=a-4\Rightarrow-3+4=a-4+4\Rightarrow1=a\Rightarrow a=1`

Then, the equation of the function is:

`f(x)=1(x-1)^2-4\Rightarrow f(x)=(x-1)^2-4`

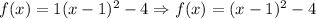
Now, to find the other function in terms of f(x), we can see that the function, g(x), is the result of reflecting f(x) in the y-axis, f(-x), and then reflecting the resulting function in the x-axis, -f(-x), as follows:

We have that the two functions are:

`f(x)=(x-1)^2-4`
`g(x)=-f(-x)\Rightarrow g(x)=-((-x-1)^2-4)`
`g(x)=-(-x-1)^2+4`

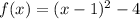
If we graph both functions, we have:

Therefore, the equation of g in terms of the function f is:

`g(x)=-f(-x)`

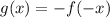
[Option D.]