Question

Use the graph below to write the formula (in factored form) for a polynomial of least degree.negative odd degree function. y intercept at 2. x intercept at -1 and 2.If you have a non-integer coefficient then write it as a fraction. Organize factors (left to right) from smallest zero to largest. Answer:

Answer 1

- This graph has two x-intercepts: x = -1 and 2.

- The y-intercept: y = 2.

- At x = 2 the graph passes through the axis linearly, suggesting the corresponding factors of the polynomial will be linear.

- At x = -1, the graph bounces off the x-axis at the intercept suggesting the corresponding factor of the polynomial will be second degree (quadratic).

Therefore, this gives us:

`f(x)=a(x+1)^2(x-2)`

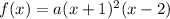
To determine the stretch factor (a), we utilize another point on the graph. We will use the y-intercept (0, 2), to solve for a:

`\begin{gathered} f(0)=a(0+1)^2(0-2) \\ 2=a(1)^2(-2) \\ 2=-2a \\ (2)/(-2)=(-2a)/(-2) \\ a=-1 \end{gathered}`

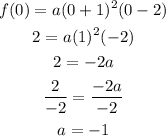
The graphed polynomial appears to represent the function:

`f(x)=-1(x+1)^2(x-2)`

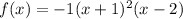
Answer:

`f(x)=-1(x-2)(x+1)^2`