Question

ORATIOS, PROPORTIONS, AND PERCENTSWord problem on proportions: Problem type 2BobEach marble bag sold by Jane's Marble Company contains 5 orange marbles for every 6 purple marbles. If a bag has 30 orange marbles, how many purplemarbles does it contain?

Answer 1

So we are told that each marble bag has 5 orange marbles for every 6 purple ones. Then the proportion of orange marbles is:

`(5)/(6)`

This proportion has to be the same for any amount of marbles in a bag. If we use x for the number of purple marbles we are looking for we have that the proportion of orange marbles in a bag with 30 orange marbles is given by:

`(30)/(x)`

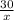
As I stated before, this proportion has always the same value so we can equalize both expressions:

`(5)/(6)=(30)/(x)`

We need to solve this for x. We can multiply x to both sides of the equation:

`\begin{gathered} (5)/(6)\cdot x=(30)/(x)\cdot x \\ (5)/(6)x=30 \end{gathered}`

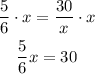
Then we multiply both sides by 6/5:

`\begin{gathered} (6)/(5)\cdot(5)/(6)x=(6)/(5)\cdot30 \\ x=36 \end{gathered}`

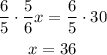
Then the answer is that the bag contains 36 purple marbles.