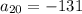What us the 20th term of the arithmetic sequence?2, -5, -12, -19,...

Question

asked Nov 24, 2023 74.2k views

1 Answer

Ricardo Anjos · Answer 1 · 2023-11-29T13:59:26+0000

Answer:

The 20th term is;

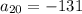
Step-by-step explanation:

Given the arithemetic sequence;

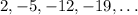
$2,-5,-12,-19,\ldots$

The first term is 2;

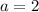
The common difference d is;

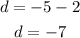
$\begin{gathered} d=-5-2 \\ d=-7 \end{gathered}$

The nth term of an arithemetic sequence can be calculated using the formula;

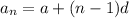
substituting for the 20th term, n=20;

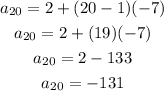
$\begin{gathered} a_(20)=2+(20-1)(-7) \\ a_(20)=2+(19)(-7) \\ a_(20)=2-133 \\ a_(20)=-131 \end{gathered}$

Therefore, the 20th term is;