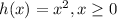We have the following functions
![\begin{gathered} f(x)=\sqrt[]{x}=x^{(1)/(2)} \\ g(x)=(\sqrt[]{x})^3=x^{(3)/(2)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/taj0tkzp71aoaxtzic6hfuqprepb40gnc6.png)
We want to find:
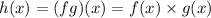
If we substitute and do the product:
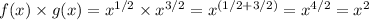
Our h(x) function is:
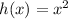
We still need to be careful about the domain. The restrictions from the f(x) and g(x) function remains, then the function h(x) will be defined only for
x >= 0.