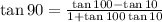Use the sum and difference identities to rewrite the following expression as a trigonometric function of a single number.tan(100°) – tan(10)1 + tan(100°)tan (10)

Question

asked Jun 6, 2023 47.2k views

1 Answer

Eimmer · Answer 1 · 2023-06-10T23:53:35+0000

$\tan 90$

Given the trigonometric function:

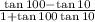
$(\tan 100-\tan 10)/(1+\tan 100\tan 10)$

According to the double angle rule in trigonometry identity;

$\tan (A-B)=(\tan A-\tan B)/(1+\tan A\tan B)$

Comparing both expressions, you can see that:

A = 100⁰

B = 10⁰

This shows that the given trigonometry identity is equivalent to:

$\tan (100-10)=(\tan100-\tan10)/(1+\tan100\tan10)$

Next is to write the trigonometry function tan(100-10) as a function of single number;

Since tan(100-10) = tan 90, hence;

$\tan 90=(\tan100-\tan10)/(1+\tan100\tan10)$