x=7
length= 4
width=15
Step-by-step explanation
Step 1
we have a rectangle,
Let
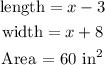
now, the area of a rectangle is given by
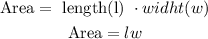
replace
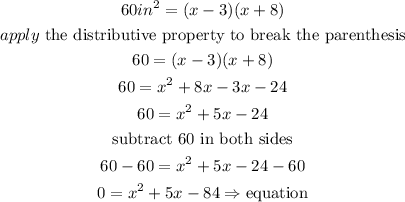
Step 2
solve the equation :
to solve this equaition, we can use the quadratic formula
remember
![\begin{gathered} \text{if} \\ ax^2+bx+c=0 \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/f7h52y5j6q9ttiwewb9l3jjtcn2y79ai6h.png)
then, let
a=1
b=5
c=-84
replace to solve for x
![\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x=\frac{-5\pm\sqrt[]{5^2-4\cdot1\cdot-84}}{2\cdot1} \\ x=\frac{-5\pm\sqrt[]{361}}{2} \\ x=(-5\pm19)/(2) \\ \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/j9bhq996314hsx3phpg3dc4yfggylr2ehe.png)
so
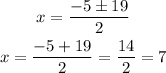
the only valid answer is the positive one, so
x=7
Step 3
finally, to find teh length and width, replace the x value
so
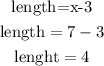
and
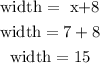
I hope this helps you