Question

2. Find the area of the smaller sector formed byZNMP. Round your answer to the nearesthundredth. (2pts)NM7010 mArea of smaller sector:

Answer 1

We can find the area of a sector of a circle using the following equation:

`A=(N)/(360)(\pi\cdot r^2)`

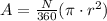
where N is the angle in degrees and r is the radius. In this case, we have the following:

`\begin{gathered} N=70 \\ r=10 \end{gathered}`

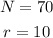
using the formula, we get:

`\begin{gathered} A=(70)/(360)(3.14\cdot(10)^2)=(70)/(360)(314)=61.1 \\ \Rightarrow A=61.1m^2 \end{gathered}`

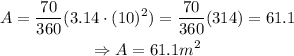
therefore, the area of the sector formed by angle NMP is 61.1m^2