Question

In the figure below, a radius and tangent line are drawn in black. The radius has alength of 8, and the tangent line bycontains a segment of length 5, as shown.Find the length of C.

Answer 1

Given the figure, we can deduce the following information:

radius= 8

tangent line =5

To determine the length of C, we first redraw the figure as shown below:

Next, we use Pythagorean theorem:

`c^2=a^2+b^2`

where:

a=5

b=8

c=C

Then, we plug in what we know:

`\begin{gathered} c^(2)=a^(2)+b^(2) \\ C^2=5^2+8^2 \\ Simplify \\ C^2=89 \\ C=√(89) \end{gathered}`

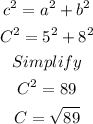
Therefore, the answer is:

`√(89)`