Answer:
The percent markup is: 9.0%
SOLUTION
Problem Statement
The question tells us a boat dealer bought a sailboat for $13,400 and sold it for $14600. We are asked to find the percent markup on the boat.
Method
In order to solve this question, we need to understand the meaning of percentage markup.
Definition:
A percentage markup is a profit from selling a good or service, which is a percentage of the cost.
Thus, the selling price of a sailboat is equal to the cost price of the sailboat plus a percentage of the cost price (i.e. markup)
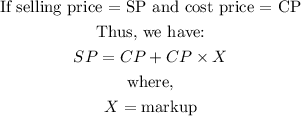
Implementation
Thus, we can find the markup using the formula given above.

Thus, the markup percentage is gotten by just multiplying the value of X by 100 %
Percent Markup is:
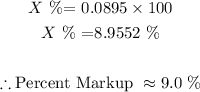
Final Answer
The percent markup is: 9.0%