Question

A pipe that is closed at one end can be made to resonate by a tuning at a length of 0.25 m. The next resonant length is 0.75 m. If the speed of sound is 338 m/s, calculate:A. The wavelength of the sound emitted by the tuning fork.B. The frequency of the tuning fork

Answer 1

Given data:

* The fundamental length of pipe is,

`L_1=0.25\text{ m}`

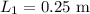
* The next resonant length of pipe is,

`L_2=0.75\text{ m}`

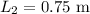
* The speed of the sound is v = 338 m/s.

Solution:

The fundamental length of the pipe in terms of the wavelength is,

`L_1=(1)/(4)\lambda`

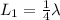
The second resonant length of the pipe in terms of wavelength is,

`L_2=(3)/(4)\lambda`

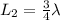
Substracting both the values,

`\begin{gathered} L_2-L_1=(3)/(4)\lambda-(1)/(4)\lambda \\ L_2-L_1=(2)/(4)\lambda \\ L_2-L_1=(1)/(2)\lambda \end{gathered}`

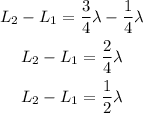
Substituting the known values,

`\begin{gathered} 0.75-0.25=(1)/(2)*\lambda \\ 0.5=(1)/(2)*\lambda \\ \lambda=1\text{ m} \end{gathered}`

Thus, the value of the wavelength of sound emitted by the tuning fork is 1 meter.

(b). The frequency of the sound is,

`\begin{gathered} v=f\lambda \\ f=(v)/(\lambda) \\ f=(338)/(1) \\ f=338\text{ Hz} \end{gathered}`

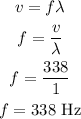
Thus, the frequency of sound is 338 Hz.