Answer:
47.9 degrees.
Step-by-step explanation:
The diagram representing this problem is drawn and attached below:
The length of the shadow cast by the building is labeled x above.
Using trigonometric ratios:
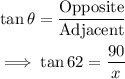
Next, solve the equation for x:
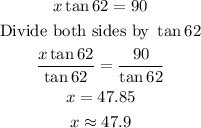
Thus, the length of the shadow cast by a building 90 ft tall is 47.9 degrees (correct to the nearest tenth).