To find the limit given we need to divide the numerator and denominator by the highest power of x in the denominator. We notice that the highest power is x squared, then we divide by this power:
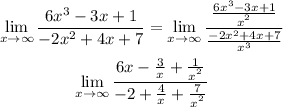
Now, since:
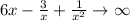
and
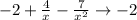
we conclude that:
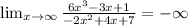
(Remember that this does not mean that the limit exist, this just means that the values of the function become small as x becomes large. This is a short way to express that)
Now, remember that an horizontal asymptote is defined as:
The line y=L is called a horizontal asymptote of the curve y=f(x) if either
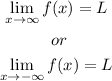
Since this is not the case we conclude that his is not a horizontal asymptote.
Now a vertical asymptote is defined as:
The vertical line x=a is called a vertical asymptote of the curve y=f(x) if at least one of the following statements is true:
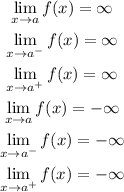
Since this is not the case we conclude that his is not a vertical asymptote.