Question

The number of bacteria in a certain population increases according to a continuous exponential growth model, with a growth rate parameter of 15% per hour. An initial sample is obtained from this population, and after five hours, the sample has grown to 2265 bacteria. Find the number of bacteria in the initial sample. Round your answer to the nearest integer.Note: This is a continuous exponential growth model.And though the growth rate parameter is 15% per hour, the actual growth is not 15% each hour.

Answer 1

The population is increasing by a continuous exponential growth model. Then, it follows the next formula:

`P(t)=P_0e^(rt)`

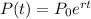
Where P=2265, Po= ?, r=15% = 0.15 and t=5.

P = final population

P0= initial population

r= rate

t= time

Replacing with the given values:

`2265=P_0e^(0.15\ast5)`

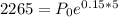
Solve for Po:

`P_0=(2265)/(e^(0.15\ast5))`

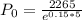
Then

`P_0=1070`

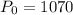
Hence, the number of bacteria in the initial sample is 1070.

(The value is rounded to the nearest integer).