Question

11. A 65 degree object is placed in a 385 degree oven. The object reaches 130 degrees in 32 minutes. A. What is the temperature of the object after 45 minutes? Be sure to show your work, including the work to get the model. Only solutions using formulas from the 4.6 lecture notes will receive credit.B. How long does it take to reach 230 degrees? Be sure to show your work.

Answer 1

The formula for exponential growth is as follows:

`P=P(0)e^(kt)`

In the problem, the following are the given data:

`\begin{gathered} P(0)=65 \\ P=130 \\ t=32 \end{gathered}`

Substitute the values into the equation and then solve for k. Thus, we have the following.

`\begin{gathered} 130=65e^(k(32)) \\ 130=65e^(32k) \\ (130)/(65)=e^(32k) \\ 2=e^(32k) \\ \ln 2=\ln (e^(32k)) \\ \ln 2=32k \\ k=(\ln2)/(32) \\ k\approx0.02166 \end{gathered}`

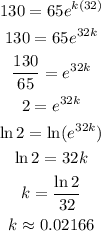
This means that the growth rate is approximately 2.166%.

To identify the temperature at 45 minutes, substitute 45 min to the value of t in the formula. Use 65 for P(0) and 0.02166 for k. Thus, we have the following.

`\begin{gathered} P=P(0)e^(kt) \\ P=65e^((0.02166)(45)) \\ P=65e^(0.9747) \\ P\approx65(2.65037) \\ P\approx172.274 \end{gathered}`

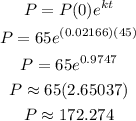
This means that the object will reach approximately 172.274° in 45 minutes.

To identify the time it will take to reach 230°, substitute 65 for P(0), 230 for P, and 0.02166 for k. Thus, we obtain the following:

`\begin{gathered} P=P(0)e^(kt) \\ 230=65e^(0.02166t) \\ (230)/(65)=e^(0.02166t) \\ \ln (230)/(65)=\ln (e^(0.02166t)) \\ \ln (230)/(65)=0.02166t^{} \\ t=(\ln (230)/(65))/(0.02166) \\ t\approx(1.26369)/(0.02166) \\ t\approx58.342 \end{gathered}`

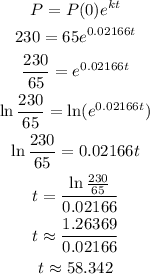
Therefore, it will take approximately 58.342 minutes to reach 230°.