Given the system of equations:
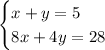
We will use the elimination method to solve the system of equations
To eliminate (y), multiply the first equation by (-4) which is the opposite of the coefficient of (y) for the second equation
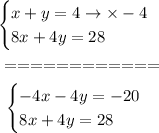
Add the equations, note (y) will be eliminated
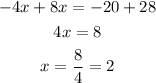
Substitute with (x) into the first equation to find (y)
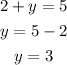
So, the solution to the system is the point (2, 3)
The answer will be option C. (2, 3)