We are given the rational expression below;
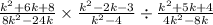
To begin, we shall refine the right side of the expression. Note that when a fraction is being divided, we invert the fraction (turn upside down) and then multiply. Therefore, for the right side of the expression we would have;
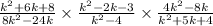
Our next step is to factorize each part of the entire expresion as follows;
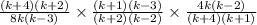
We now have the factors as shown in the equation above.
With these we can write out the restrictions for this expression as follows;
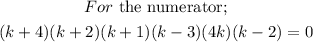
Therefore, we now have the restrictions at;
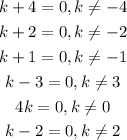
Note very carefully that the factors in the denominator are the same as those in the numerator. Hence, we would not need to repeat the steps as shown for the numerator. The restrictions would be exactly the same for both numerator and denominator.
The restrictions therefore are;
ANSWER:

We can now simplify.
It is important to note that we must state the restrictions BEFORE cancelling out factors;
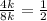
After cancelling out ALL common factors in both numerator and denominator, we are left with 4k/8k which finally simplifies into 1/2
SIMPLIFIED:
