Hello there. To solve this question, we'll have to remember some properties about functions.
Given the cost function C(q) on the production of q goods is given by the expression:
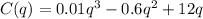
And suppose the price of selling is 10 dollars per unit.
The profit function is given by P(q), that is the difference between the amount sold and the cost, i.e.
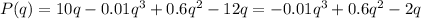
We want to maximize this function, considering that when we increase the price by 1 dollar, we sell less units, that is, from 38 units, we sell 37.
We start plugging q = 38 into it
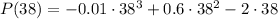
Then we introduce a new variable r that is the amount that should be increased/decreased (the sign will tell us) such that when q turns to q - r, the selling price goes from 10 to 10 + r, so that
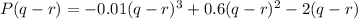
Plugging q as 38, call P(38 - r) = F(r) such that
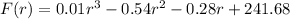
Now we take its derivative with respect to r
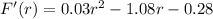
This might be zero, so that we find the critical points of F
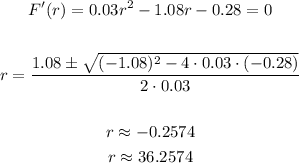
And taking the second derivative of F, we get
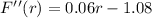
Evaluating it at the roots of F'(r), we get
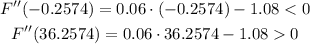
So we maximize F(r) at r = -0.2574 or approximately -0.26
And we say that P(q - r) is maximized when the price is 10 + r = $9.74, giving $241.72 of profit.
The negative sign of r tell us that the price should decrease by 0.26 dollars.