We're going to solve the system of equations:
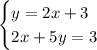
Using substitution.
For this, all we need to do is to replace the first equation in the second one:
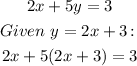
Now, we could solve this linear equation:
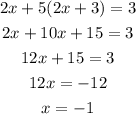
Therefore, x=-1.
Now, to find the value of y we could replace x=-1 in any of both equations:
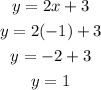
Therefore, x = -1 , y = 1, and the solution of the system is (x,y)=(-1,1).