Question

The price of 5 citrons and 3 fragrant wood apples is 27 units. The price of 3 citrons and 5 fragrant wood apples is 29 units. Find the price of a citron and the price of a wood apple.

Answer 1

The Solution.

Let the price of a citron be represented with x, and the price of a fragrant wood apple be y.

So, the first sentence in the question gives the equation below:

`5x+3y=27\ldots eqn(1)`

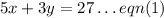
Similarly, the second sentence in the question gives the equation below:

`3x+5y=29\ldots eqn(2)`

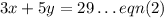
Solving the above pair of equations simultaneously using the Elimination Method:

We shall eliminate the term in x;

So, we shall multiply through eqn(1) by 3, we get

`\begin{gathered} 3(5x+3y=27) \\ 15x+9y=81\ldots eqn(3) \end{gathered}`

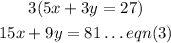
Similarly, we shall multiply through eqn(2) by 5, we get

`\begin{gathered} 5(3x+5y=29) \\ 15x+25y=145\ldots eqn(4) \end{gathered}`

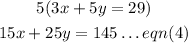
Subtracting eqn(3) from eqn(4), we have

`\begin{gathered} 15x+25y=145 \\ -(15x+9y=81) \end{gathered}`

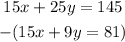
We get:

`16y=64`

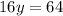
Dividing both sides by 16, we get

`\begin{gathered} (16y)/(16)=(64)/(16) \\ \\ y=4 \end{gathered}`

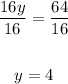
To find x, we shall substitute 4 for y in eqn(1):

`\begin{gathered} 5x+3(4)=27 \\ 5x+12=27 \end{gathered}`

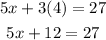
Collecting the like terms, we get

`\begin{gathered} 5x=27-12 \\ 5x=15 \end{gathered}`

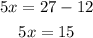
Dividing both sides by 5, we get

`\begin{gathered} (5x)/(5)=(15)/(5) \\ \\ x=3 \end{gathered}`

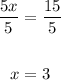
Therefore, the price of a citron is 3 units, and the price of a fragrant wood apple is 4 units.