Question

The angle of elevation to the top of a building in Seattle is found to be 3 degrees from the ground at a distance of 1.5miles from the base of the building. Using this information, find the height of the building. Draw a picture to represent this situation and show your work.

Answer 1

0.079 miles = 417.12 feet

Step-by-step explanation

The building forms a right triangle with the floor and the observer,

We know the measure of one interior angle of the triangle and the length of its adjacent side. We have to find the length of the opposite side, so we use the tangent of the angle,

`\tan 3\text{\degree}=(h)/(1.5mi)`

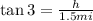
Solve for h,

`h=1.5mi\tan 3\text{\degree}\approx0.079mi`

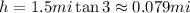
Hence, the height of the building is approximately 0.079 miles or 417.12 feet