Solve each system of equations 2x + 3y = 9 x - 2y = 1 Ordered pair

Question

asked Jun 18, 2023 126k views

1 Answer

SIMMORSAL · Answer 1 · 2023-06-23T03:34:23+0000

Given the equation system

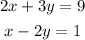
$\begin{gathered} 2x+3y=9 \\ x-2y=1 \end{gathered}$

First step is to write of the equations in terms of one of the variables, for example I'll write the second equation in terms of x:

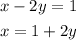
$\begin{gathered} x-2y=1 \\ x=1+2y \end{gathered}$

Second step is to replace the expression obtained for x in the first equation:

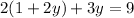
Solve the parentheses using the distributive property of multiplications:

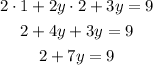
$\begin{gathered} 2\cdot1+2y\cdot2+3y=9 \\ 2+4y+3y=9 \\ 2+7y=9 \end{gathered}$

Pass the 2 tothe other side of the equation by subtracting it from both sides of the = sign

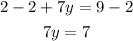
$\begin{gathered} 2-2+7y=9-2 \\ 7y=7 \end{gathered}$

And divide both sides by 7

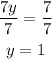
$\begin{gathered} (7y)/(7)=(7)/(7) \\ y=1 \end{gathered}$

Replace it in the first expression obtained to determine the value of x:

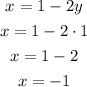
$\begin{gathered} x=1-2y \\ x=1-2\cdot1 \\ x=1-2 \\ x=-1 \end{gathered}$

This sistem of equations has one solution at x=-1 and y=1