Question

a circle has its center at (1,2). it has a radius of 5 units. which point does not lie on the circle.

Answer 1

The standard form of a circle is

`(x-h)^2+(y-k)^2=r^2`

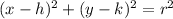
Where

(h, k) is the center

r is the radius

Given,

Center (1, 2) and Radius 5, we can write >>>

`(x-1)^2+(y-2)^2=5^2`

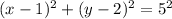
This is the equation of the circle. We plug in each point (x, y) into the circle equation and see which one does not satisfy the equation.

Checking (4, 6)

`\begin{gathered} (4-1)^2+(6-2)^2\stackrel{?}{=}5^2 \\ 9+16\stackrel{?}{=25} \\ 25=25 \end{gathered}`

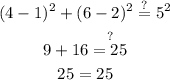
Checking (-2, -2)

`\begin{gathered} (-2-1)^2+(-2-2)^2\stackrel{?}{=}5^2 \\ 9+16\stackrel{?}{=}25 \\ 25=25 \end{gathered}`

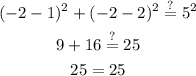
Checking (1, 6)

`\begin{gathered} (1-1)^2+(6-2)^2\stackrel{?}{=}5^2 \\ 0+16\stackrel{?}{=}25 \\ 16\\eq25 \end{gathered}`

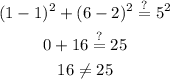
So, the point (1, 6) doesn't lie on the circle!