To answer this question, we need to use a cumulative standard normal distribution table. In the standard normal distribution, we have that the mean is equal to zero and the standard deviation is equal to 1.
Part A
To find c for a standard normal distribution, we need to find the value of c for which the right area at this z-score is equal to 0.2181. Then, if we consult a cumulative standard normal distribution table, the value of the cumulative probability is at the left, we have to subtract 0.2181 from 1 to obtain the left area of the distribution:
![P(zThen, the value for c for which we have a cumulative probability of 0.7819 is about z = 0.78. Then, c is about c = 0.78<h2>Part B</h2><p>To find this area, we need to find the cumulative probabilities for P(z<-2.867) and P(z<2.867), and then we will need to subtract:</p>[tex]P(-2.867If we use a graphing calculator, we obtain:[tex]P(z<-2.867)=0.0020719150629]()
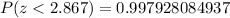
Then, we have:
![P(-2.867If we round the result to four decimal places, we have that:[tex]P(-2.867Part C<p>To answer this part, we need to find the following probability area:</p>[tex]P(-0.59The area outside from this interval is:[tex]1-P(-0.59And then, we need to]()
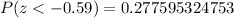
![P(-0.59Then<p></p>[tex]1-P(-0.59If we round the result to four decimal places, we have 0.5552, and we can say:[tex]0.5552\Rightarrow55.52\%]()
Part D
To answer this part of the question, we have the following situation:
Since the normal distribution is symmetrical, we need to divide the probability by 2. The result will be the distance from the mean (0). We know that the cumulative probability for the mean is P(z<0) = 0.5000:
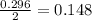
And from this, we can say that the values are 0.148 units from the mean. Since the cumulative probability for the mean is P(z<0) = 0.5000, we can add the latter as follows:
![P(zIf we consult the value for z in the cumulative standard normal distribution, we have that <strong>z is about z = 0.38</strong>. Therefore, we have that b is equal to 0.38 and -b = -0.38:[tex]undefined]()
Part E
To find the probability for those values of z, we can proceed as follows:
[tex]P(1.26Then[tex]P(1.26If we round the result to four decimals, we have:[tex]P(1.26