Question

I need help finding the slop of the line in simplest form

Answer 1

The Solution:

The question requires that we draw a line representing a Rise and another line representing a Run, and thereafter find the slope of the line in its simplest form.

From the given graph in the question, we have the rise and run as below:

To find the slope of the line in its simplest form, we shall use the formula below:

`\text{ Slope =}(y_2-y_1)/(x_2-x_1)`

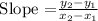
We shall pick the coordinates of two points in the line as below:

`(1,-2)\text{ and (7,0)}`

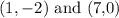
In this case,

`\begin{gathered} x_1=1 \\ y_1=-2 \\ x_2=7 \\ y_2=0 \end{gathered}`

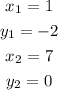
Substituting these values in the formula above, we get

`\text{ Slope = }(0-(-2))/(7-1)=(0+2)/(6)=(2)/(6)=(1)/(3)`

Therefore, the slope of the line is 1/3