Question

There is a line that includes the point (4, 1) and has a slope of 1 slope-intercept form? of What is its equation in 4 Write your answer using integers, proper fractions, and improper fractions in simplest form.

Answer 1

The form of the linear equation is

`y=mx+b`

m is the slope

b is the y-intercept

Since the slope of the line is 1, then

m = 1

Substitute it in the form of the equation above

`\begin{gathered} y=(1)x+b \\ y=x+b \end{gathered}`

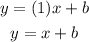
To find b substitute x and y in the equation by the coordinates of a point on the line

Since the line contains the point (4, 1), then put

x = 4 and y = 1

`1=4+b`

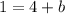
Subtract 4 from both sides to find b

`\begin{gathered} 1-4=4-4+b \\ -3=b \end{gathered}`

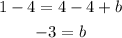
Substitute the value of b in the equation

`\begin{gathered} y=x+(-3) \\ y=x-3 \end{gathered}`

The equation of the line is y = x - 3