Question

In the figure below, what is the length of W? Also, the 12 is 12 cm.

Answer 1

In this case, we can identify two similar triangles like this:

We can formulate the following ratios between the sides of the two triangles:

`(b2)/(b1)=(h2)/(h1)`

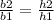
Where b1 and h1 are the base and height of the larger triangle (blue) and b2 and h2 are the base and height of the smaller triangle (red). By replacing 16 for b2, 20 for b1 (16 + 4), w for h2 and 12 for h1 we get:

`(16)/(20)=(w)/(12)`

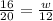
From this equation, we can solve for w, to get:

`\begin{gathered} (16)/(20)=(w)/(12) \\ (16)/(20)*12=(w)/(12)*12 \\ (16*12)/(20)=w \\ 9.6=w \\ w=9.6 \end{gathered}`

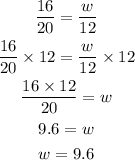
Then, the length of w is 9.6 cm