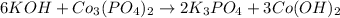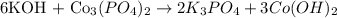
The strategy for balancing chemical equations algebraically is as follows:
1. Write a different letter coefficient in front of each compound in the equation
2. Write algebraic expressions or rules for each element that equate its atoms on the LHS and RHS
3. Substitute and simplify to obtain a rule that equates only two letter coefficients that you can solve
3. Substitute the values into the other rules to obtain the balancing coefficients
So for this equation:
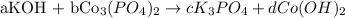
Now that we have given each compound a coefficient, we will solve for a, b, c and d.
Next, applying the Conservation of Mass, which tell us that the total number of atoms of each element must be the same on both sides, write algebraic rules for each element.
K: a = 3c
OH: a = 2d
Co: 3b = d
PO4: 2b = c
There are too many unknown here, so we need to eliminate some.
If a = 2 (Given)
Then:
2 = 3c
c = 2/3
2 = 2d
d = 1
3b = d
3b = 1
b = 1/3
So a = 2, b = 1/3, c = 2/3 and d = 1
We have to get rid of the fraction by multiplying by 3
Therefore: a = 2 x 3 = 6
b = 1/3 x 3 = 1
c = 2/3 x 3 = 2
d = 1 x 3 = 3
Now we can substitute these numbers to the equation: