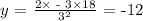Question

I need to solve those problems but I don’t understand how to can u help me please.

Answer 1

Step-by-step explanation:

a) From the question, we have it that y joint varies as m an n then inversely with the square of d

Let us have k as the variation constant

We have this as:

`\begin{gathered} y\text{ }\alpha\text{ }(mn)/(d^2) \\ \\ y\text{ = k}\cdot(mn)/(d^2) \end{gathered}`

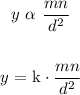
b) We want to find the variation constant value

To get this, we use the values supplied in the question

`\begin{gathered} 12\text{ = k}*(3*8)/(2^2) \\ k\text{ = }(12*4)/(24) \\ k\text{ = 2} \end{gathered}`

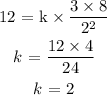
c) We want to find the value of y given the second condition set

mathematically, we have that as:

`y\text{ = }\frac{2*\text{ - 3}*18}{3^2}\text{ = -12}`