1 Answer

Eile · Answer 1 · 2023-01-29T03:53:24+0000

Answer:

x = 2

Explanation:

Given equation:

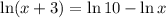
$\ln(x+3)=\ln 10 - \ln x$

$\textsf{Apply the log quotient law}: \quad \ln a - \ln b= \ln (a)/(b)$

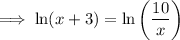
$\implies \ln(x+3)=\ln\left((10)/(x)\right)$

$\textsf{Apply the log equality law}: \quad \textsf{if }\: \ln a= \ln b\:\textsf{ then }\:a=b$

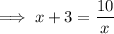
$\implies x+3=(10)/(x)$

Multiply both sides by x:

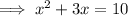
$\implies x^2+3x=10$

Subtract 10 from both sides:

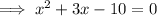
$\implies x^2+3x-10=0$

Split the middle term:

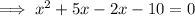
$\implies x^2+5x-2x-10=0$

Factor the first two terms and the last two terms separately:

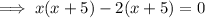
$\implies x(x+5)-2(x+5)=0$

Factor out the common term (x+5):

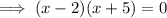
$\implies (x-2)(x+5)=0$

Apply the zero-product property:

$\implies x-2=0\implies x=2$

$\implies x+5=0 \implies x=-5$

As logs of negative numbers cannot be taken, the only valid solution is:

Please log in or register to add a comment.