Question

Can you please help me solve for the test statistics and p value and conclusion

Answer 1

From the conclusion of the hypothesis:

`\begin{gathered} H_o\colon\mu=48.0 \\ H_1\colon\mu>48.0 \end{gathered}`

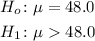
The null hypothesis is that mean number is equal to 48

The alternate hypothesis is that mean number is greater than 48

Option A is the correct answer

Hence the test statistics will be given as

`\begin{gathered} t_{\text{test}}=\frac{\bar{x}-\mu}{\frac{s}{\sqrt[]{n}}} \\ t_{\text{test}}=\frac{57.7-48}{\frac{16.1}{\sqrt[]{10}}} \\ t_{\text{test}}=1.91 \end{gathered}`

The p - value of the t - test above at degree of freedom of 9 is

`\begin{gathered} t_{\text{score}}=1.91 \\ df=n-1 \\ df=10-1=9 \\ p-\text{value = 0}.044 \end{gathered}`

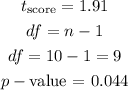
Since the p- value is greater than the significance level, do not reject the null hypothesis

So the conclusion is that

Failed to reject H₀, there is not sufficient evidence to support the claim.