Question

. Construct and Interpret a 95% confidence level. 5 poin One study claims students get 8 hours of sleep a night, on average. One professor asks a random sample of 32 students, "How much sleep did you get last night?" Here are the data in hours) 9 6 6 7.5 6 6 5 8.5 6 5.5 6.5 6 4 8 6 6.5 7 7 4 4.5 3 6 5 7 10 8 9 7 7 9

Answer 1

Using a mean and standard deviation calculator we can see that

`\text{ the sample mean }\bar{x}=6.75`
`\text{ the sample standard deviation }s=1.8184`

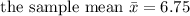
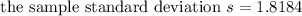
We now calculate the standard error

`\begin{gathered} \text{ standard error }=\frac{s}{\sqrt[]{n}} \\ \text{Where} \\ s=\text{ the sample standard deviation} \\ n=\text{ the sample size} \end{gathered}`

In this case,

n = 32,

`\text{standard error = }\frac{1.8184}{\sqrt[\square]{32}}=\text{ 0.3215}`

We now calculate the critical probability p*

`\text{ critical probability }=1-(\alpha)/(2)`
`\begin{gathered} \alpha=0.05 \\ \text{ Therefore} \\ \text{ critical probability }=1-(0.05)/(2)=0.975 \end{gathered}`

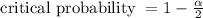
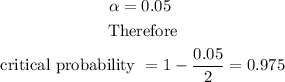
Next, we find the degree of freedom df

`df=32-1=31`

We can now find the critical value. The critical value is the t value having degrees of freedom equal to df and a cumulative probability equal to the critical probability (p*).

Using a t-score calculator, we find that the critical value is 2.040

We will now find the margin of error (ME)

`\begin{gathered} ME\text{ = critical value x stansard error} \\ ME\text{ = }2.040\text{ x }0.3215\text{ = 0.6559} \end{gathered}`

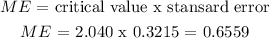
confidence interval is = mean

`\text{confidence interval = mean}\pm\text{ margin of error= }6.75\pm0.6559\text{ }`

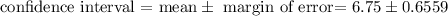
Confidence interval is (6,75-0.6559, 6,75+0.6559)

Confidence interval is (6.0941, 7.4059).

This means that the professor is 95% certain that the average hour of sleep of each student falls within the interval (6.0941, 7.4059).